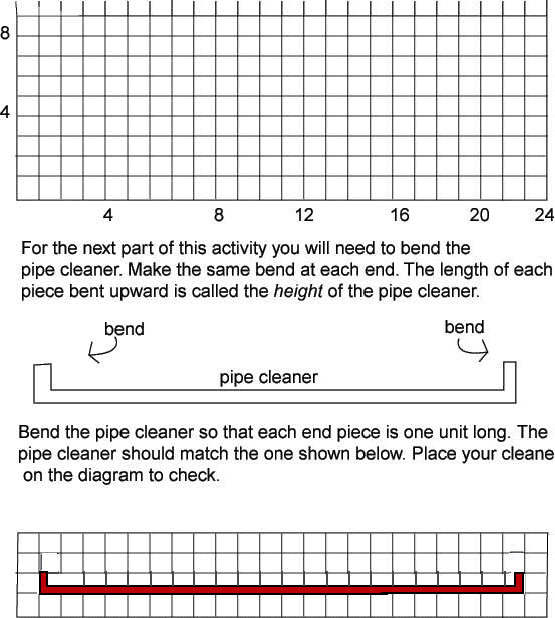
Measure the pipe cleaner by using the grid below. How many units long is the pipe cleaner? _____________

2a. What is the height of the pipe cleaner in the figure?_________

2b. The bottom part of the pipe cleaner is called the base. What is the length of he base in the figure?

2c. The area of the figure is the number of squares above the pipe cleaner, but no higher than the tops of the pieces bent upward. What is the area of the figure?_________

3a. Now straighten the pipe cleaner. Bend it again so that the length of each bent upward is 2. What is the length of the base of the pipe cleaner now?__________

3b. Place the pipe cleaner on the grid and find the area.___________

4. Continue straightening and bending the pipe cleaner so that the length of the piece bent upward is one unit larger each time. Record the results in the table below. You may stop when there is no longer enough pipe cleaner to continue.

5. The height of the pipe cleaner varies from step to step in your table. For this reason the height is called a variable. What other variables are there in this activity?

6. Something that doesn't vary is called a constant. Are there any constants in this activity?

7a. The largest possible value of a variable is called it's maximum. What is the maximum value for the area in this activity?

7b. What is the value of the height that produced the maximum area? _____________

7c. Does this value of the height also produce a maximum value for the base?_____________

8. Study the height and the base columns in your table. Is there a relationship between the base and the height? Can you find a rule that describes how to obtain the base in your table from the height?

9. Find a rule for calculating the area from the base and the height.

10. Find a rule for calculating the area from the height alone.