|
This activity was developed by a
student or students at Mainland High School which is located in Daytona Beach, FL.
It is still a "work in progress" with editing and improvements yet to come.
 Inflate one balloon until it feels tight, but not stretched.
(This seems so subjective… Your goal is that the balloon be inflated as big as
possible while still being able to be covered with an inflated balloon.) Inflate one balloon until it feels tight, but not stretched.
(This seems so subjective… Your goal is that the balloon be inflated as big as
possible while still being able to be covered with an inflated balloon.)
 Tie a knot in the "neck" of a balloon
Tie a knot in the "neck" of a balloon
 Clip the "neck" of another balloon as shown in the illustration below.
Clip the "neck" of another balloon as shown in the illustration below.
 One Student should stretch the clipped balloon while the partner stuffs the
inflated balloon inside. Once this is done (the WORST is over), another balloon is clipped
and used to cover the inflated balloon ball.
One Student should stretch the clipped balloon while the partner stuffs the
inflated balloon inside. Once this is done (the WORST is over), another balloon is clipped
and used to cover the inflated balloon ball.
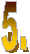 Continue covering until all the balloons have been used.
Continue covering until all the balloons have been used.
 |
An oblong balloon can be "rounded" by
positioning the open end of the clipped balloon in different spot each time. Clip the
"ring" off <image> the remaining band and use it to decorate and shape the
balloon ball. |
Number of balloons used to make your
bouncing balloon:_________
|
|

|
Drop Height
X |
Bounce Height
Y |
Y/X |
| ________
cm |
________
cm |
________ |
| ________
cm |
________
cm |
________ |
| ________
cm |
________
cm |
________ |
Average of
this column |
________ |
|
|

|
Drop Height
X |
Bounce Height
Y |
Y/X |
| ________
cm |
________
cm |
________ |
| ________
cm |
________
cm |
________ |
| ________
cm |
________
cm |
________ |
Average of this column |
________ |
 ….find the average
of your two averages! ________ ….find the average
of your two averages! ________
We will call this number the constant of your function.


Under the best of scientific testing conditions, the
function of your Balloon Ball would have been a Linear Function,
meaning that it’s graph would be on a line.
Let’s see how close you came to optimum conditions by
graphing your X’s and Y’s from both trials…..
 …..how did you do?
Are your results an approximation of a line? What are some casual factors? …..how did you do?
Are your results an approximation of a line? What are some casual factors?

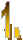
Once again, what was the constant of your
function?
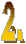 What was the constant of your partner's function? What was the constant of your partner's function?
How would you account for the difference in your constant and
your partner's constant? (Give at least two possible causes)
How could you use your constant to make predictions concerning your
bouncing balloon?
Let’s try! If the drop height were _______, what would
you predict the bounce height to be?

How did your experimental results compare with your predicted results?
Explain any similarities or differences.
|





 ….find the average
of your two averages! ________
….find the average
of your two averages! ________ 

 …..how did you do?
Are your results an approximation of a line? What are some casual factors?
…..how did you do?
Are your results an approximation of a line? What are some casual factors?
